How does a decision happen?

Note:
Utility function depends not only on the action but also in the situation; e.g., in economic situation it is the market value, in evolutionary purpose it is the reproductive success, e.t.c.
Tragedy of the Commons (TOC)
The tragedy of the commons (TOC) is an unfortunate situation where a shared resource collapses due to overexploitation by selfish individuals. To use a finite common resource successfully and for an extended period, individuals should carefully use it. The population's size also plays an essential role in determining the fate of the resource that they are harvesting for living. The environment is not always predictable, and some noise is also present there. To study the whole picture, one should not forget the effect of noise. I want to make a compact study to predict the TOC, i.e., how a population can avert TOC and when it is inevitable.
Preventation of 'tragedy of the Commons' in the increasing population
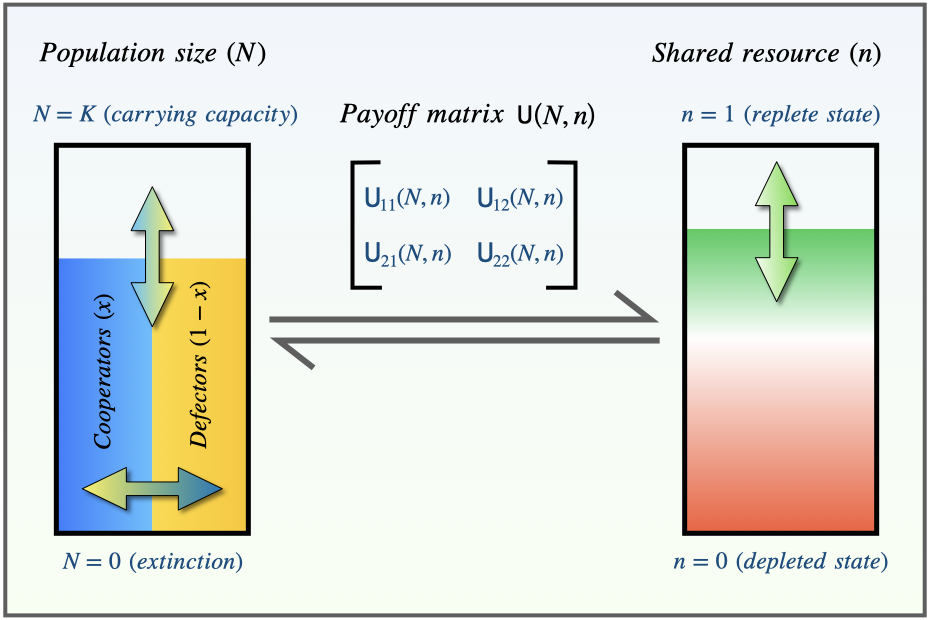
The tragedy of the commons (TOC) is an unfortunate situation where a shared resource is exhausted due to uncontrolled exploitation by the selfish individuals of a population. Recently, the paradigmatic replicator equation has been used in conjunction with a phenomenological equation for the state of the shared resource to gain insight into the influence of the games on the TOC. The replicator equation, by construction, models a fixed infinite population undergoing microevolution. Thus, it is unable to capture any effect of the population growth and the carrying capacity of the population although the TOC is expected to be dependent on the size of the population. Therefore, in this paper, we present a mathematical framework that incorporates the density dependent payoffs and the logistic growth of the population in the eco-evolutionary dynamics modeling the game-resource feedback. We discover a bistability in the dynamics: a finite carrying capacity can either avert or cause the TOC depending on the initial states of the resource and the initial fraction of cooperators. In fact, depending on the type of strategic game-theoretic interaction, a finite carrying capacity can either avert or cause the TOC when it is exactly the opposite for the corresponding case with infinite carrying capacity.
Preventation of 'tragedy of the Commons' in the increasing population for self-renewing Resource
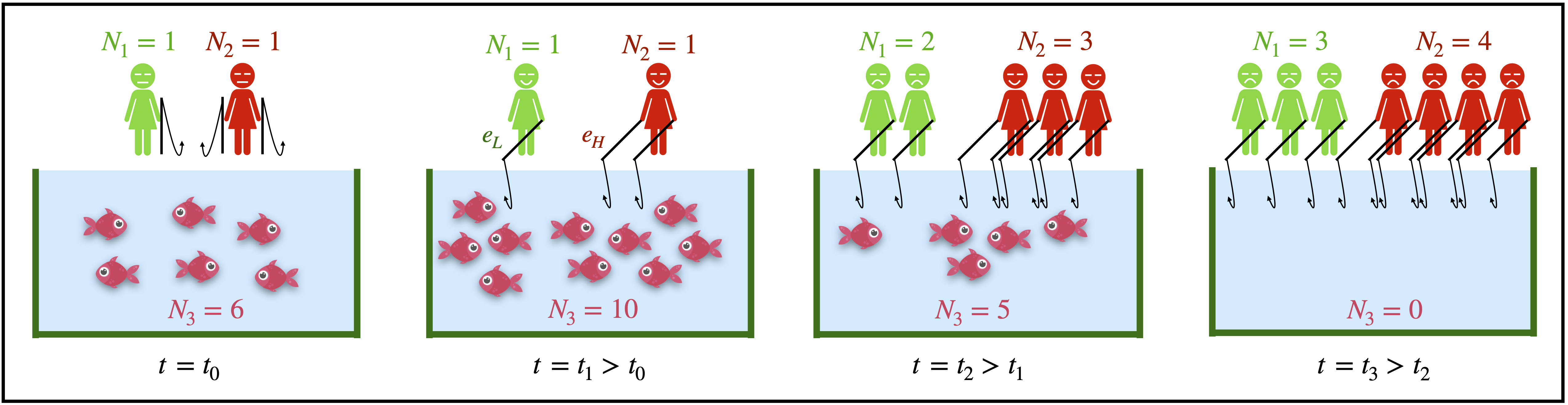
The tragedy of the commons (TOC) is a ubiquitous social dilemma witnessed in interactions between a population of living entities and shared resources available to them: The individuals in the population tend to selfishly overexploit a common resource as it is arguably the rational choice, or in case of non-human beings, it may be an evolutionarily uninvadable action. How to avert the TOC is a significant problem related to the conservation of resources. It is not hard to envisage situations where the resource could be self-renewing and the size of the population may be dependent on the state of the resource through the fractions of the population employing different exploitation rates. If the self-renewal rate of the resource lies between the maximum and the minimum exploitation rates, it is not a priori obvious under what conditions the TOC can be averted. In this paper, we address this question analytically and numerically using the setup of an evolutionary game theoretical replicator equation that models the Darwinian tenet of natural selection. Through the replicator equation, while we investigate how a population of replicators exploit the shared resource, the latter's dynamical feedback on the former is also not ignored. We also present a transparent bottom-up derivation of the game-resource feedback model to facilitate future studies on the stochastic effects on the findings presented herein.
Role of information in preventing the TOC
Broken Symmetry prevent extinction
